Stats2_seminar_3

Rethinking Statistics
Author

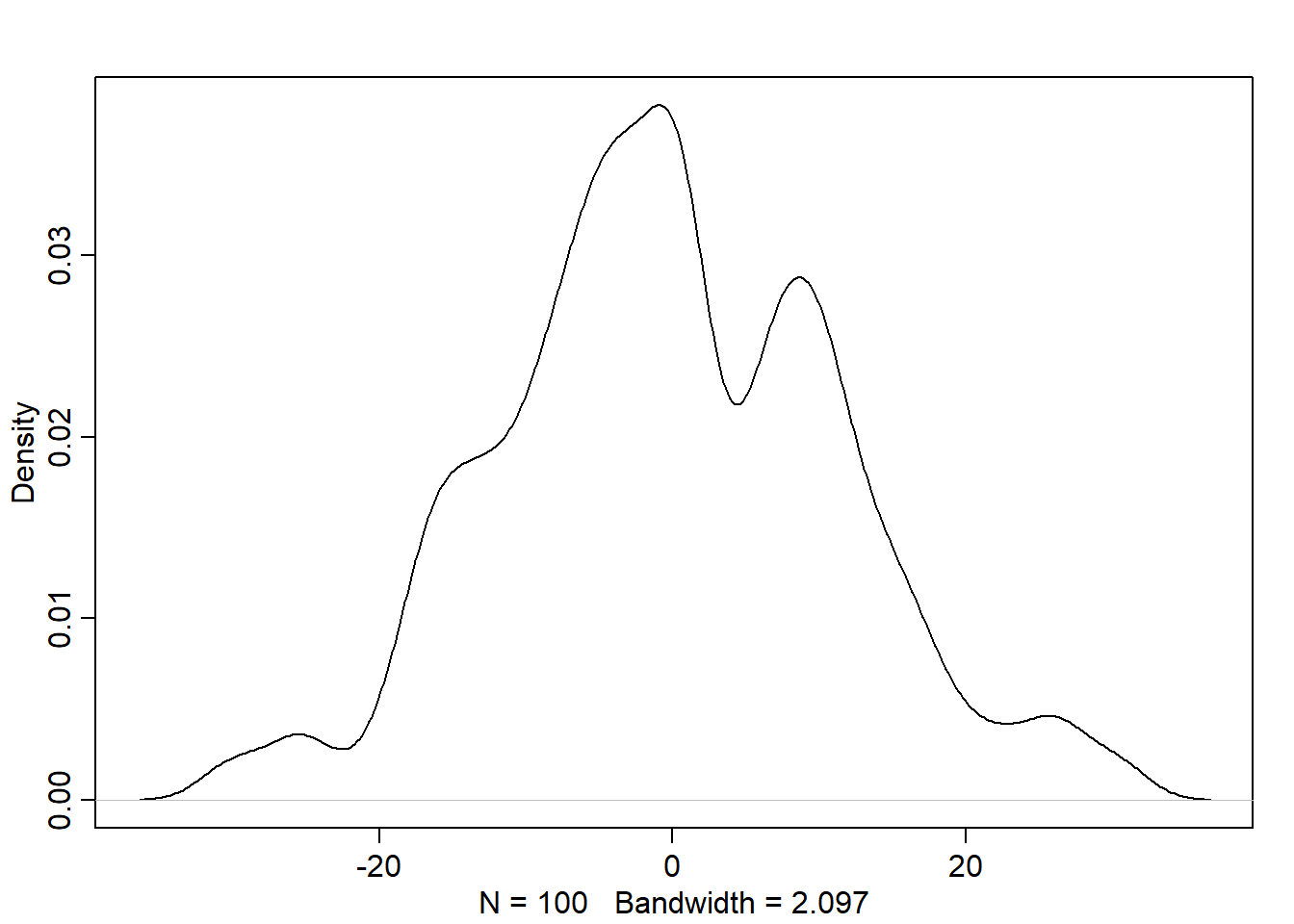
Vilgot Huhn

Published

February 22, 2025

4M1

For the model definition below, simulate observed y values from the prior (not the posterior). \[ \begin{align} y_i &\sim Normal(µ,σ) \\ µ &\sim Normal(0,10) \\ σ &\sim Exponential(1) \end{align} \]

#I think this simulates from prior.
n <- 100
sigma <- rexp(n, 1)
mu <- rnorm(n, mean = 0, sd = 10)
y <- rnorm(n, mu, sigma) #we're only plugging in values drawn from our prior.

dens(y)

4M2. Translate the model just above into a quap formula.

flist <- alist(
  y ~ dnorm(mu, sigma),
  mu ~ dnorm(0, 10),
  sigma ~ dexp(1)
)

4M3. Translate the quap model formula below into a mathematical model definition.

\[ \begin{align} y_i &\sim Normal(\mu_i,\sigma) \\ \mu_i &= a + b*x_i \\ a &\sim Normal(0,10) \\ b &\sim Uniform(0,1) \\ \sigma &\sim Exponential(1) \end{align} \]

flist <- alist(
 y ~ dnorm( mu , sigma ),
 mu <- a + b*x,
 a ~ dnorm( 0 , 10 ),
 b ~ dunif( 0 , 1 ),
 sigma ~ dexp( 1 )
 )

4H1.

The weights listed below were recorded in the!Kung census, but heights were not recorded for these individuals. Provide predicted heights and 89% intervals for each of these individuals. That is, fill in the table below, using model-based predictions.

t <- data.frame(individual = 1:5, weights = c(46.95,43.72,64.78,32.59,54.63), expected_height = rep(NA, times = 5), low_89_PI = rep(NA, times = 5), high_89_PI = rep(NA, times = 5),xbar = rep(NA, times = 5))
t
  individual weights expected_height low_89_PI high_89_PI xbar
1          1   46.95              NA        NA         NA   NA
2          2   43.72              NA        NA         NA   NA
3          3   64.78              NA        NA         NA   NA
4          4   32.59              NA        NA         NA   NA
5          5   54.63              NA        NA         NA   NA
data(Howell1)
d <- Howell1
d <- d[d$age >= 18,]
xbar <- mean(d$weight)

mdl <- quap(
  alist(
  height ~ dnorm(mu, sigma),
  mu <- a + b * (weight - xbar), #where is xbar defined? Must be part of quap built in?
  a ~ dnorm( 178, 20), 
  b ~ dlnorm(0, 1),
  sigma ~ dunif(0,50)
), data = d
)
precis(mdl)
             mean         sd        5.5%       94.5%
a     154.6013573 0.27030758 154.1693536 155.0333610
b       0.9032811 0.04192362   0.8362791   0.9702831
sigma   5.0718795 0.19115465   4.7663774   5.3773815
#post <- extract.samples( mdl ) 
#data <- c(46.95,43.72,64.78,32.59,54.63)
#for (i in data) {
 # y <- rnorm( 1e5 , post$a + post$b*i , post$sigma ) 
  #print(mean(y))
  #print(HPDI(y,prob=0.89))
#}

post <- extract.samples(mdl, n = 1000)

t$expected_height <- apply(sim(mdl, data=list(weight=t$weights)),2, mean)
#I guess we could also do it by formula.
t$low_89_PI <- apply(sim(mdl, data=list(weight=t$weights)),2, PI)[1,]
t$high_89_PI <- apply(sim(mdl, data=list(weight=t$weights)),2, PI)[2,]

t
  individual weights expected_height low_89_PI high_89_PI xbar
1          1   46.95        156.2150  147.9285   164.0839   NA
2          2   43.72        153.2816  145.8356   162.1845   NA
3          3   64.78        172.6121  164.2527   180.4767   NA
4          4   32.59        143.3276  135.4016   151.6196   NA
5          5   54.63        162.8802  155.3697   171.1801   NA

Mats suggest we should do this manually too: i.e. don’t use link() or sim()

4H2.

Select out all the rows in the Howell1 data with ages below 18 years of age. If you do it right, you should end up with a new data frame with 192 rows in it.

  1. Fit a linear regression to these data, using quap. Present and interpret the estimates. For every 10 units of increase in weight, how much taller does the model predict a child gets? Answer: 27.18372
  2. Plot the raw data, with height on the vertical axis and weight on the horizontal axis. Super impose the MAP regression line and 89% interval for the mean. Also superimpose the 89% interval for predicted heights.
  3. What aspects of the model fit concern you? Describe the kinds of assumptions you would change, if any, to improve the model. You don’t have to write any new code. Just explain what the model appears to be doing a bad job of, and what you hypothesize would be a better model.
#0.
data(Howell1)
d <- Howell1
d <- d[d$age < 18,]
#
d <- d[sample(1:nrow(d),size = 10),]
xbar <- mean(d$weight)

#1.
#challanging to chose priors for kids 0-18. I'm going with this. A tall 18 is 190cm. So half that.
#and I don't know what I'm talking about, so wide SD.
#I don't know enough to mess with the other priors but something positive so I'm keeping the dlnorm(0,10)
#and I don't know how close the relationship will be so model sigma between 0 and 10 seems fine
mdl2 <- quap(
  alist(
  height ~ dnorm(mu, sigma),
  mu <- a + b * (weight - xbar),
  a ~ dnorm( 95, 20), 
  b ~ dlnorm(0, 1),
  sigma ~ dunif(0,10)
), data = d
)
precis(mdl2)
            mean        sd       5.5%      94.5%
a     112.076281 1.5129022 109.658371 114.494191
b       3.393750 0.2158979   3.048704   3.738797
sigma   4.795944 1.0749938   3.077896   6.513992
precis(mdl2)[2,1]*10
[1] 33.9375
#2. plot MAP line and PI89
post <- extract.samples(mdl2)
weight.seq <- c(4:45)
mu <- link(mdl2, data=data.frame(weight=weight.seq))
mu.PI <- apply(mu,2,PI)
sim.heights <- sim(mdl2, data=data.frame(weight=weight.seq), post = post)
height.PI <- apply(sim.heights, 2, PI, prob = 0.97)
plot(height ~ weight, data = d, ylim = c(50,180)); curve(mean(post$a) + mean(post$b)*(x-xbar),add = TRUE); shade(mu.PI, weight.seq); shade(height.PI, weight.seq)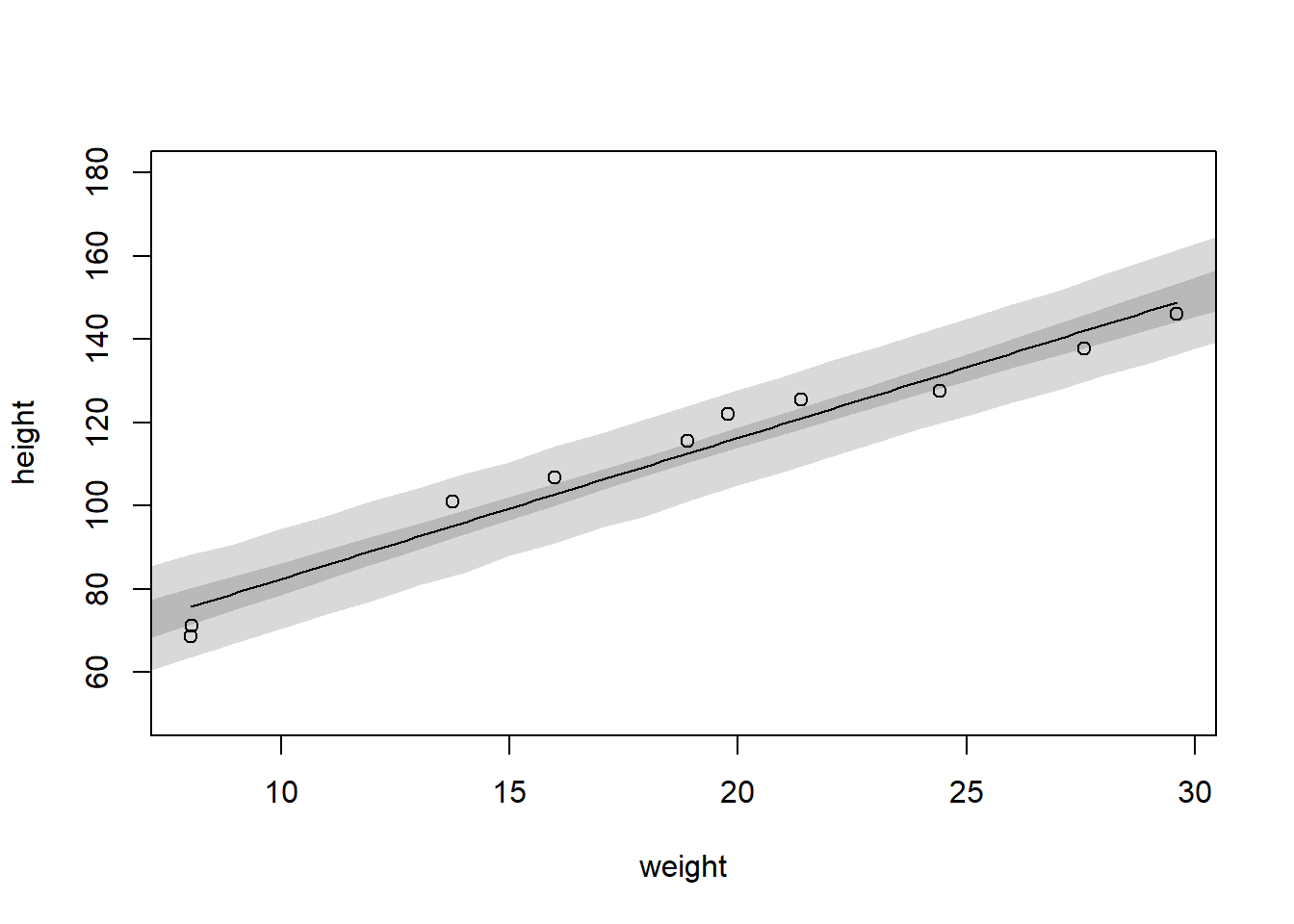

#My attempt at writing an own sim() function
#post are paired parameters drawn from the model.
weight.seq.random <- sample(weight.seq, size = 1000, replace = TRUE)
predicted_points <- rnorm(1000, mean = post$a + post$b*(weight.seq.random - xbar), sd = post$sigma)
plot(weight.seq.random, predicted_points) #don't know hot to get a PI here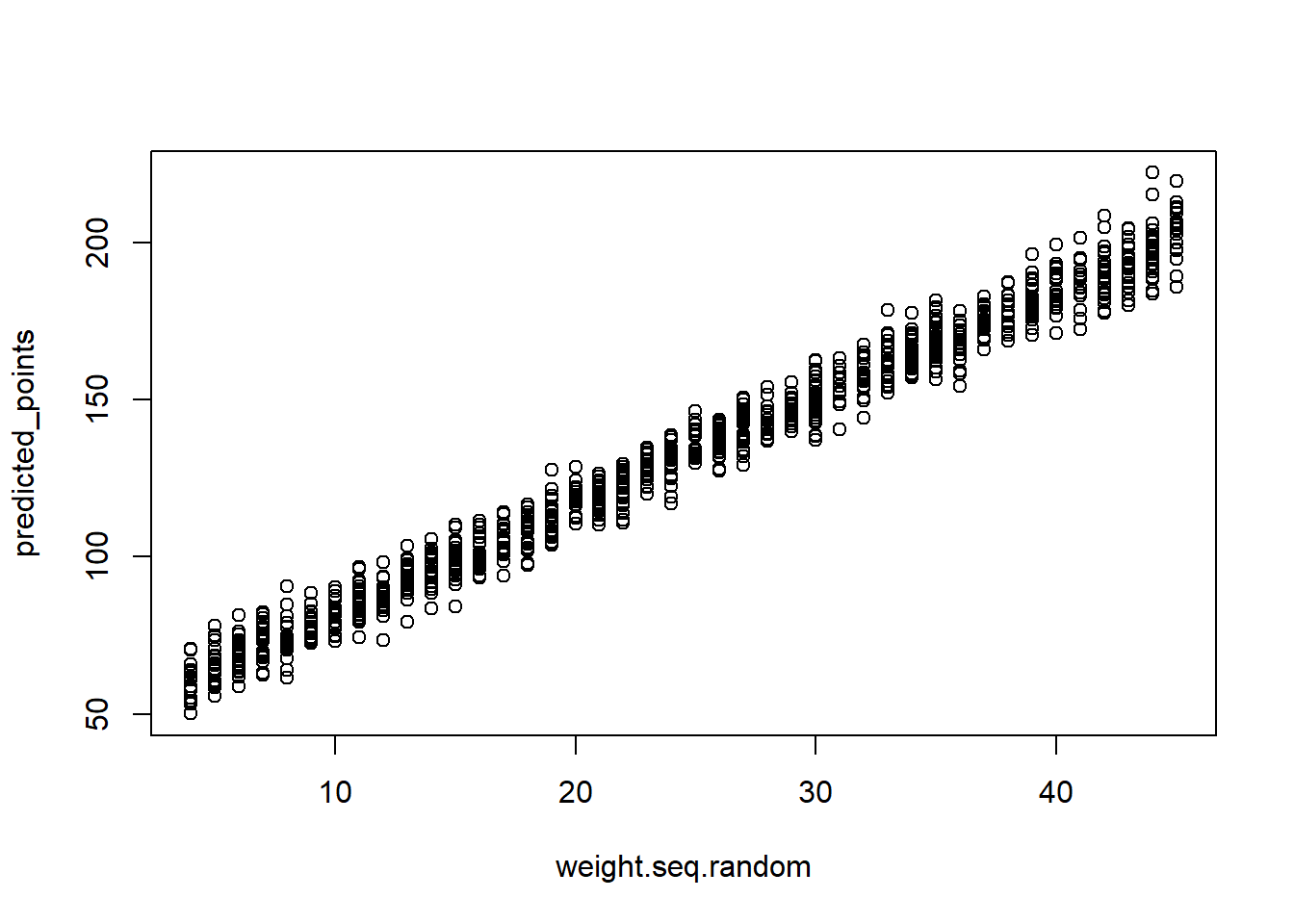

#seems the errors should propagate but it's not easy to see visually

#second attempt. my own sim for prediction intervals
n <- 1000
s <- c(5:45)
post <- rethinking::extract.samples(mdl2, n = n)
d2f <- matrix(nrow = n, ncol = 0)
  for(i in s){
    d2f <- cbind(d2f,rnorm(n, mean = post$a + post$b*(s[1+i-min(s)] - xbar), sd = post$sigma))
  } #super dumb for loop man...
my.sim.PI <- apply(d2f,2,PI)
plot(my.sim.PI[2,] - my.sim.PI[1,])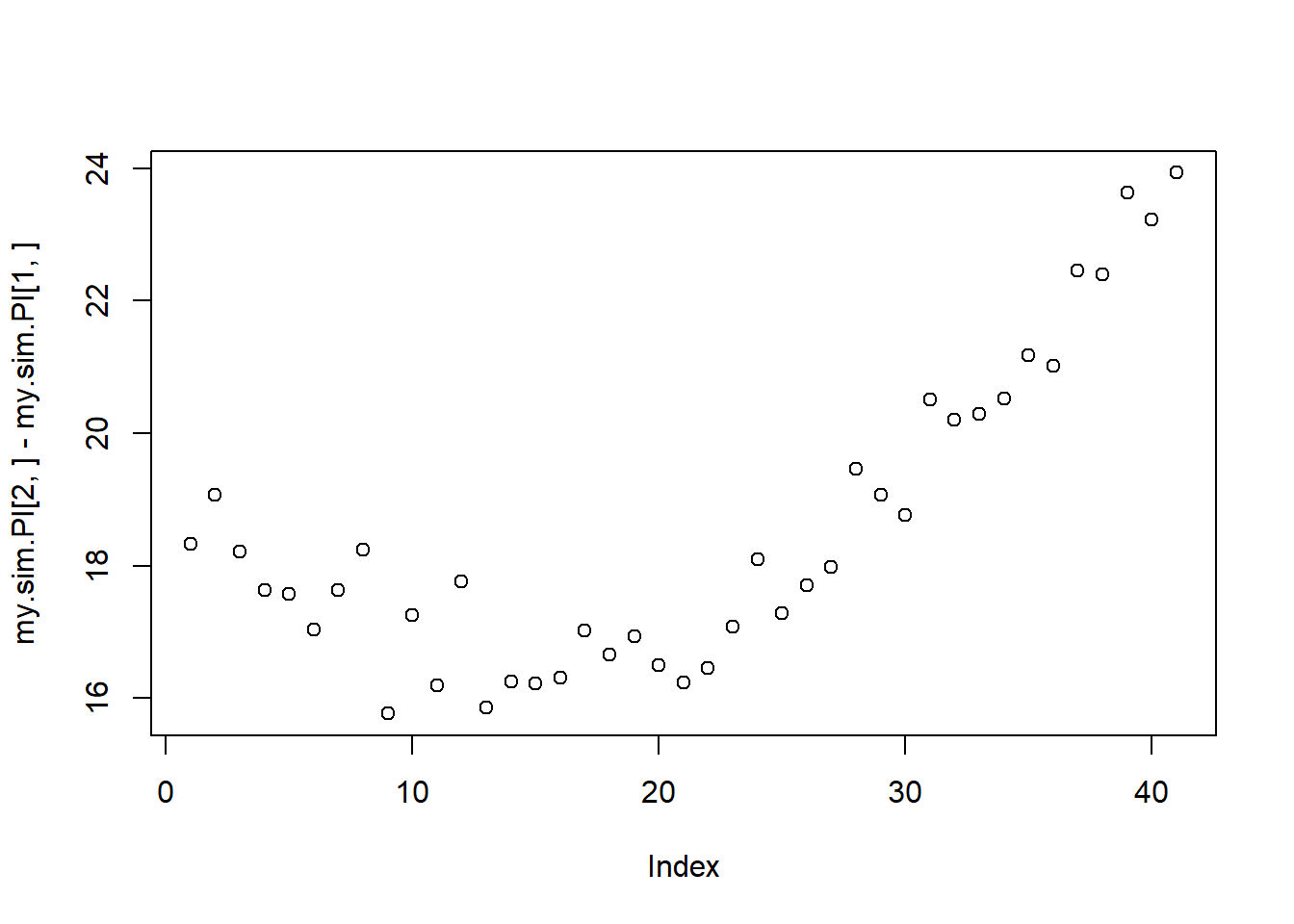

#here we can see what is less clear with the naked eye
#plot(height.PI[2,] - height.PI[1,]) 
#plot(mu.PI[2,] - mu.PI[1,])

Answer 3: I’d be concerned about how far off the MAP-line is from the data-points, especially in the middle. The relationship looks non-linear.

4H3.

Suppose a colleague of yours, who works on allometry, glances at the practice problems just above. Your colleague exclaims, “That’s silly. Everyone knows that it’s only the logarithm of body weight that scales with height!” Let’s take your colleague’s advice and see what happens.

  1. Model the relationship between height(cm)and the natural logarithm of weight(log-kg). Use the entire Howell1 data frame, all 544 rows, adults and non-adults. Fit this model, using quadratic approximation: \[ \begin{align} h_i &∼ Normal(µ_i,σ) \\ µ_i &= α+βlog(w_i) \\ α &∼Normal(178,20) \\ β &∼Log−Normal(0,1) \\ σ &∼Uniform(0,50) \end{align} \] where \(h_i\) is the height of individual i and wi is the weight (in kg) of individual i. The function for computing a natural log in R is just log. Can you interpret the resulting estimates?

  2. Begin with this plot:

data("Howell1")
d <- Howell1

mdl3 <- quap(
  alist(
  height ~ dnorm(mu, sigma),
  mu <- a + b * log(weight),#note that we're not doing "- mean(weight)" now, it wasn't in the formula for some reason.
  a ~ dnorm( 178, 20), 
  b ~ dlnorm(0, 1),
  sigma ~ dunif(0,10)
  ), data = d)
precis(mdl3)
            mean        sd       5.5%     94.5%
a     -22.871048 1.3343316 -25.003568 -20.73853
b      46.816794 0.3823358  46.205748  47.42784
sigma   5.137211 0.1558943   4.888062   5.38636
post <- extract.samples(mdl3) #using samples from the posterior (1)
weight.seq <- c(4:63)
mu <- link(mdl3, data=data.frame(weight=weight.seq))
mu.mean <- apply(mu,2,mean)
mu.PI <- apply(mu,2,PI, prob = 0.97)
sim.heights <- sim(mdl3, data=data.frame(weight=weight.seq))
height.PI <- apply(sim.heights, 2, PI, prob = 0.97)

plot(height ~ weight , data=Howell1 ,
 col=col.alpha(rangi2,0.4), main = "97% PI for mu", ylim = c(0,190) );  lines(weight.seq,mu.mean); shade(mu.PI, weight.seq)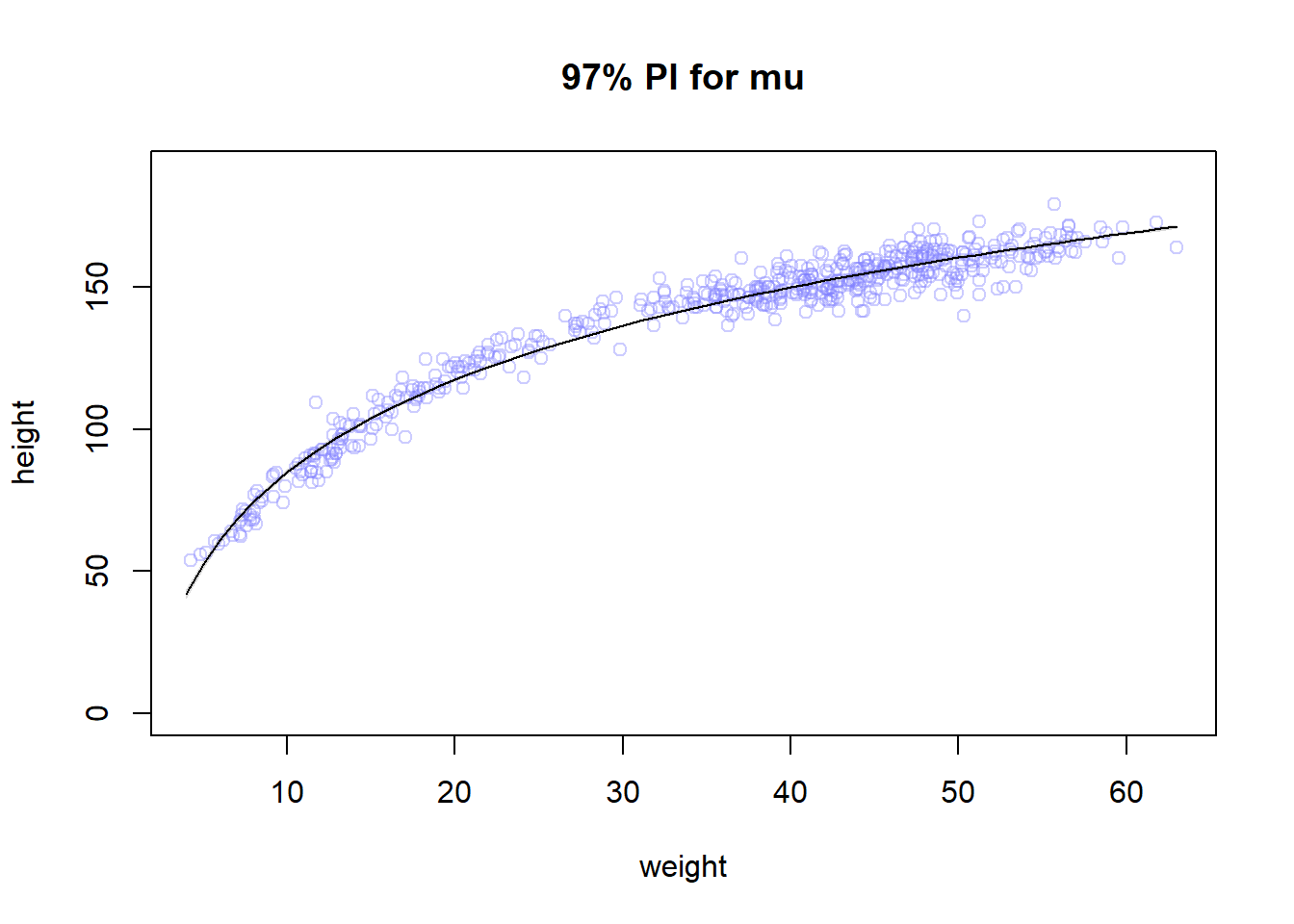

#but it's actually cooler to do it with curve actually...
plot(height ~ weight , data=Howell1 , col=col.alpha(rangi2,0.4), main = "97% PI for predicted height"  );  curve(mean(post$a) + mean(post$b) * log(x), add = TRUE);  shade(height.PI, weight.seq)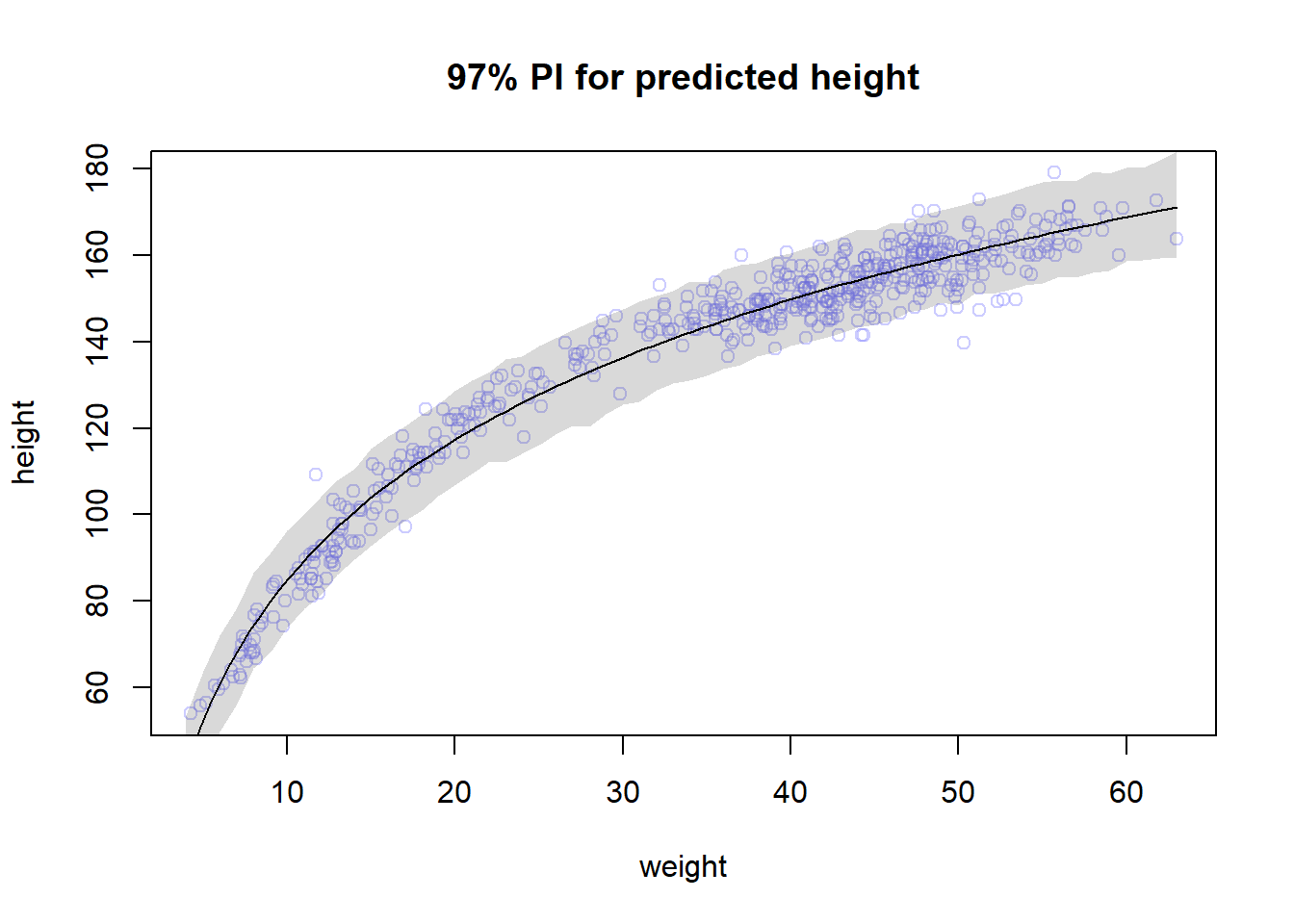

Then use samples from the quadratic approximate posterior of the model in (a) to superimpose on the plot: (1) the predicted mean height as a function of weight, (2) the 97% interval for the mean, and (3) the 97% interval for predicted heights.